In this tutorial we are going to be looking at the TanhLRScheduler in the timm library in little more detail with all the supporting hyperparameters.
from timm.scheduler.tanh_lr import TanhLRScheduler
from nbdev.showdoc import show_doc
The TanhLRScheduler as shown above accepts an optimizer and also some hyperparams which we will look into in detail below. We will first see how we can train models using the TanhLRScheduler by first using timm training script and then look at how we can use this scheduler as standalone scheduler for our custom training scripts.
To train models using the TanhLRScheduler we simply update the training script args passed by passing in --sched tanh parameter alongside the necessary hyperparams. In the next section we will also look at how each of the hyperparams update the TanhLRScheduler.
The training command to use TanhLRScheduler looks something like:
python train.py ../imagenette2-320/ --sched tanh
Let's now look at the associated hyperparams and how that updates the annealing schedule.
This is the optimizer that will be used for the training process.
from timm import create_model
from timm.optim import create_optimizer
from types import SimpleNamespace
model = create_model('resnet34')
args = SimpleNamespace()
args.weight_decay = 0
args.lr = 1e-4
args.opt = 'adam'
args.momentum = 0.9
optimizer = create_optimizer(args, model)
This optimizer object created using create_optimizer is what get's passed to the optimizer argument.
The number of epochs to schedule the hyperparameter for.
The lower bound denoted by L in the paper.
The upper bound as denoted by U in the paper.
NOTE: L and U indicate the lower and upper bounds of the interval [L, U] for the function tanh(x).
Defaults to 1.0. Similar to SGDR it updates schedule by increasing the time for annealing.
from matplotlib import pyplot as plt
def get_lr_per_epoch(scheduler, num_epoch):
lr_per_epoch = []
for epoch in range(num_epoch):
lr_per_epoch.append(scheduler.get_epoch_values(epoch))
return lr_per_epoch
num_epoch = 50
scheduler = TanhLRScheduler(optimizer, t_initial=num_epoch, t_mul=1.)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch*3)
plt.plot([i for i in range(num_epoch*3)], lr_per_epoch, label="With `t_mul=1.`");
scheduler = TanhLRScheduler(optimizer, t_initial=num_epoch, t_mul=2.)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch*3)
plt.plot([i for i in range(num_epoch*3)], lr_per_epoch, label="With `t_mul=1.`");
As we can see in the example, the second schedule that starts at epoch 50 takes twice as long for the learning to be decreased to the minimum value.
Defaults to 1e-5. The minimum learning rate to use during the scheduling. The learning rate does not ever go below this value.
When decay_rate > 0 and <1., at every restart the learning rate is decayed by new learning rate which equals lr * decay_rate. So if decay_rate=0.5, then in that case, the new learning rate becomes half the initial lr.
num_epoch = 50
scheduler = TanhLRScheduler(optimizer, t_initial=num_epoch, decay_rate=1.)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch*2)
plt.plot([i for i in range(num_epoch*2)], lr_per_epoch);
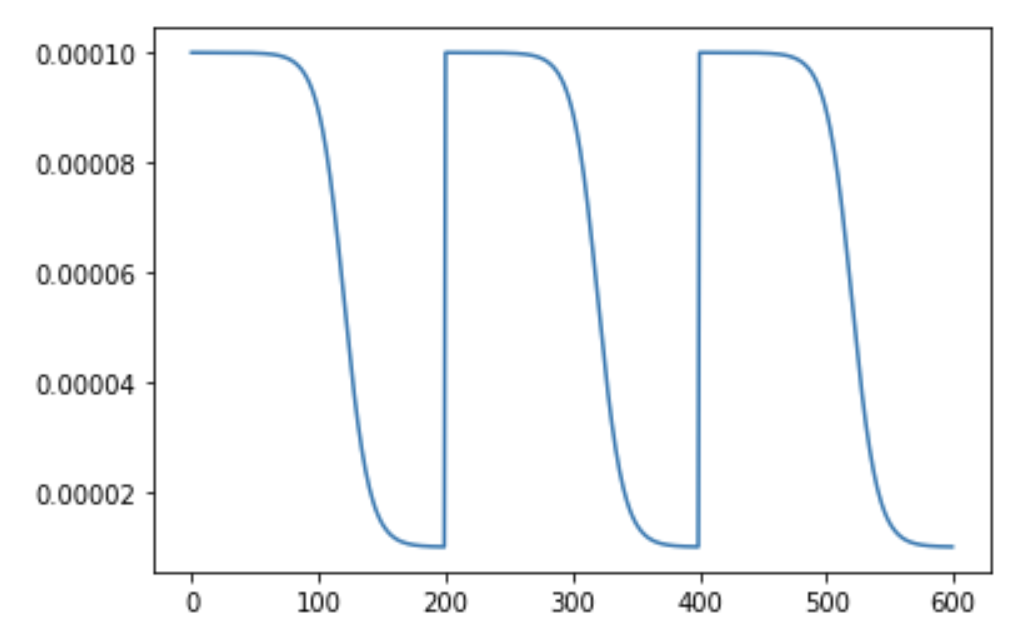
num_epoch = 50
scheduler = TanhLRScheduler(optimizer, t_initial=num_epoch, decay_rate=0.5)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch*2)
plt.plot([i for i in range(num_epoch*2)], lr_per_epoch);
Defines the number of warmup epochs.
The initial learning rate during warmup.
num_epoch = 50
scheduler = TanhLRScheduler(optimizer, t_initial=num_epoch, warmup_t=5, warmup_lr_init=1e-5)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
plt.plot([i for i in range(num_epoch)], lr_per_epoch, label="With warmup");
num_epoch = 50
scheduler = TanhLRScheduler(optimizer, t_initial=num_epoch)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
plt.plot([i for i in range(num_epoch)], lr_per_epoch, label="Without warmup", alpha=0.8);
plt.legend();
As we can see by setting up warmup_t and warmup_lr_init, the cosine scheduler first starts with a value of warmup_lr_init, then gradually progresses up to the initial_lr set in the optimizer which is 1e-4. It takes warmup_t number of epochs to go from warmup_lr_init to initial_lr.
Defaults to False. If set to True, then every new epoch number equals epoch = epoch - warmup_t.
num_epoch = 50
scheduler = TanhLRScheduler(optimizer, t_initial=num_epoch, warmup_t=5, warmup_lr_init=1e-5)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
plt.plot([i for i in range(num_epoch)], lr_per_epoch, label="Without warmup_prefix");
num_epoch = 50
scheduler = TanhLRScheduler(optimizer, t_initial=num_epoch, warmup_t=5, warmup_lr_init=1e-5, warmup_prefix=True)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
plt.plot([i for i in range(num_epoch)], lr_per_epoch, label="With warmup_prefix");
plt.legend();
In the example above we can see how the warmup_prefix updates the LR annealing schedule.
The number of maximum restarts in TanhLRScheduler.
num_epoch = 50
scheduler = TanhLRScheduler(optimizer, t_initial=num_epoch, cycle_limit=1)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch*2)
plt.plot([i for i in range(num_epoch*2)], lr_per_epoch);
num_epoch = 50
scheduler = TanhLRScheduler(optimizer, t_initial=num_epoch, cycle_limit=2)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch*2)
plt.plot([i for i in range(num_epoch*2)], lr_per_epoch);
If set to False, the learning rates returned for epoch t are None.
num_epoch = 50
scheduler = TanhLRScheduler(optimizer, t_initial=num_epoch, t_in_epochs=False)
lr_per_epoch = get_lr_per_epoch(scheduler, num_epoch)
lr_per_epoch[:5]
Add noise to learning rate scheduler.
The amount of noise to be added. Defaults to 0.67.
Noise standard deviation. Defaults to 1.0.
Noise seed to use. Defaults to 42.
If set to True, then, the an attributes initial_lr is set to each param group. Defaults to True.